Introducción
La cantidad de movimiento, momento lineal, ímpetu, es una magnitud física fundamental de tipo vectorial que describe el movimiento siendo la velocidad un vector mientras que la masa es escalar, teniendo como un vector con la misma dirección y sentido que la velocidad. La masa suele permanecer constante, por lo que lo que suele cambiar es la velocidad y si cambia la velocidad es que hay aceleración, y si hay aceleración es que hay una fuerza neta actuando sobre el objeto pero depende del tiempo en el que actúe la fuerza.
Entonces:
- Si una fuerza no muy grande se aplica durante poco tiempo, se producirá un cambio pequeño de su cantidad de movimiento.
- Pero si esa misma fuerza la aplico durante un tiempo más largo, el cambio será mayor. Es decir, la variación de la cantidad de movimiento depende de la fuerza y del intervalo de tiempo.
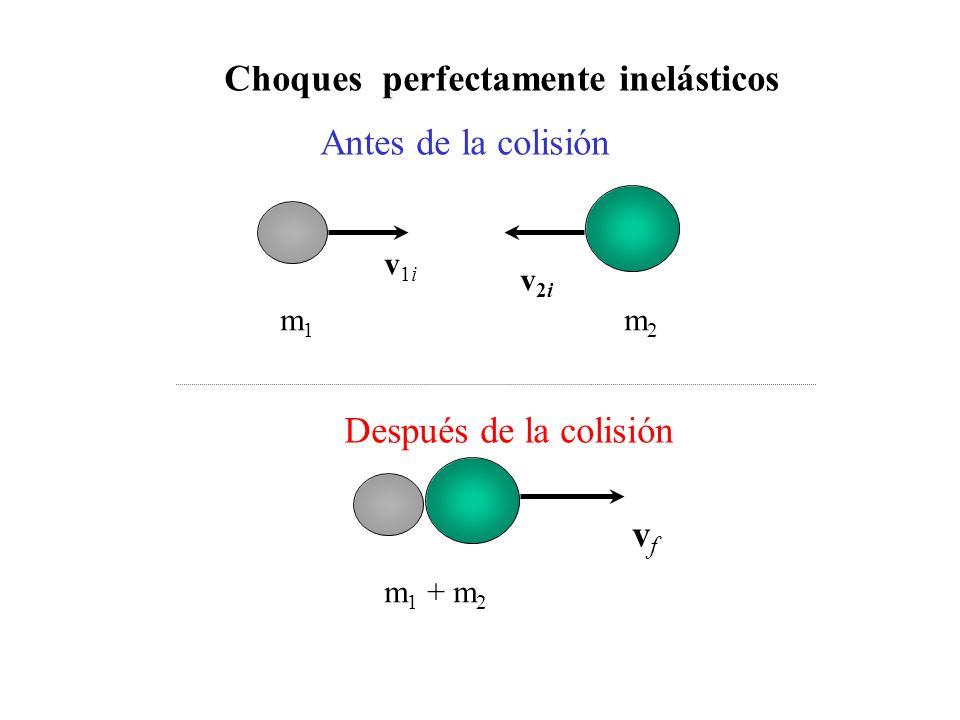
La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa.
El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento. Es el producto de la masa de un objeto por la velocidad del mismo y esta se mide en kg·m/s, tiene la misma unidad que el impulso aunque sean conceptos diferentes.