MOVIMIENTO ARMÓNICO SIMPLE

 INTRODUCIÓN

 

Decimos que una partícula o sistema tiene movimiento armónico simple (m.a.s) cuando vibra bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio. Entonces, que dicho cuerpo es un oscilador armónico.

Características del movimiento armónico simple:

1. Vibratorio: El cuerpo oscila en torno a una posición de equilibrio siempre en el mismo plano
2. Periódico: El movimiento se repite cada cierto tiempo denominado periodo (T). Es decir, el cuerpo vuelve a tener las mismas magnitudes cinemáticas y dinámicas cada T segundos
3. Se describe mediante una función sinusoidal (seno o coseno indistintamente)

Magnitudes del movimiento armónico simple:

• Amplitud, A: Elongación máxima. Su unidad de medidas en el Sistema Internacional es el metro (m).
• Frecuencia. f: El número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación / segundo = 1 s-1.
• Periodo, T: El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
• Frecuencia angular, velocidad angular o pulsación, ω : Representa la velocidad de cambio de la fase del movimiento. Se trata del número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ).

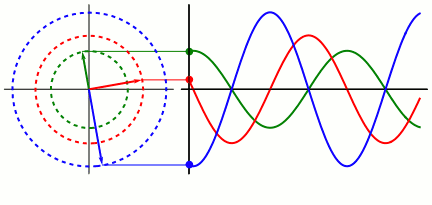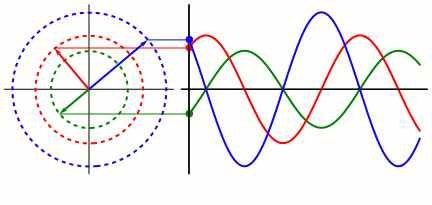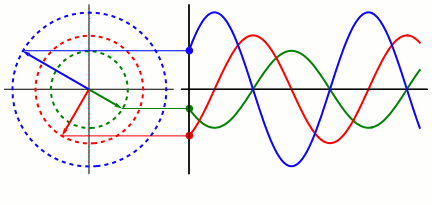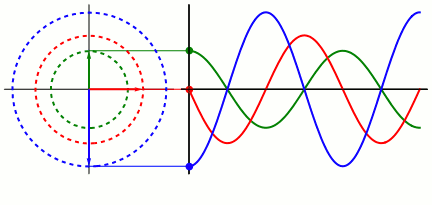
Cinemática de un M.A.S.

En un movimiento rectilíneo, dada la posición de un móvil, obtenemos la velocidad derivando respecto del tiempo y luego, la aceleración derivando la expresión de la velocidad. La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la ecuación                      

                                                     x=A·sen(ωt+φ)

Dinámica de un M.A.S.

Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.

En un resorte 

Los sistemas masa-resorte sin fricción verticales y horizontales oscilan de forma idéntica alrededor de una posición de equilibrio si sus masas y resortes son iguales.

Sin embargo, en los resortes verticales, debemos recordar que la gravedad estira o comprime el resorte más allá de su longitud natural desde la posición de equilibrio. Después de encontrar la posición de desplazamiento, podemos establecerla como el punto donde y=0, y tratar el resorte vertical tal como lo haríamos con un resorte horizontal. La Figura 1 a continuación muestra la posición de reposo de un resorte vertical y la posición de equilibrio del sistema resorte-masa después de que se ha estirado una distancia d.

En un péndulo simple 

Un péndulo se define como una partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable. Si la partícula se desplaza a una posición (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar. El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. 

Las fuerzas que actúan sobre la partícula de masa m son dos

• el peso mg

• la tensión T del hilo

Cuando el péndulo se encuentra en reposo, en vertical, permanece en equilibrio ya que la fuerza peso es contrarrestada por la tensión en la cuerda. 

Además, cuando se separa de la posición de equilibrio la tensión contrarresta solo a la componente normal del peso, siendo la componente tangencial del peso la fuerza resultante. Esta fuerza es la responsable de que aparezca una aceleración ( F = m · a ) que trata de devolver al péndulo a su posición de equilibrio.